fertyu.blogg.se

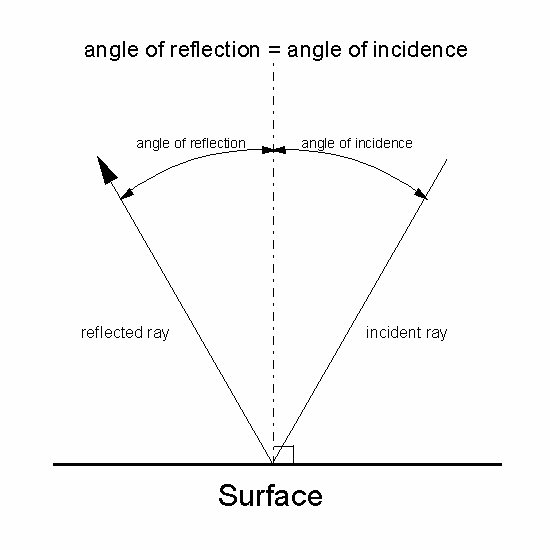
Corresponding sides are sides that extend between the same two angles in each triangle. For any two similar triangles, corresponding sides on those triangles are in the same ratio. It should now be clear that these two triangles are similar triangles, since each of the two triangles has the same three internal angles. So, for both of the triangles in our diagram, we’ll give this third angle the same label of 𝜙. This means that 𝜙 one must equal 𝜙 two. So, 𝜙 one is equal to 90 degrees minus 𝜃, and 𝜙 two is also equal to 90 degrees minus 𝜃. And we find that 𝜙 two is equal to 90 degrees minus 𝜃. We can rearrange this and simplify it in exactly the same way as we did for the orange triangle. Since the three internal angles of this blue triangle must add to 180 degrees, then we have that 𝜃 plus 𝜙 two plus 90 degrees is equal to 180 degrees. In this case, we’ll call the third angle 𝜙 two. Now, we can do the same thing for the blue triangle. Rearranging this expression, we get that 𝜙 one is equal to 180 degrees minus 90 degrees minus 𝜃, which we can also just write as 90 degrees minus 𝜃. So, we have that 𝜃 plus 𝜙 one plus 90 degrees is equal to 180 degrees. We know that the sum of the internal angles for this triangle must be equal to 180 degrees. So, for the orange triangle, we’ll label this third angle as 𝜙 one. To do this, we need to recall that the sum of internal angles in a triangle is equal to 180 degrees. We can also work out what the third angle must be for each of the triangles.

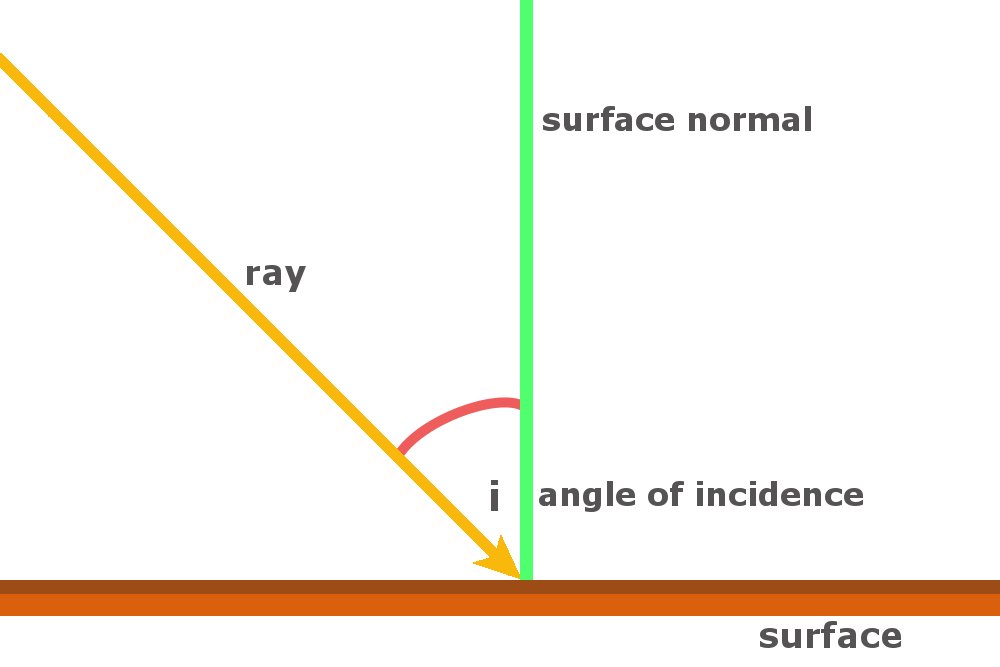
So, since both of these angles have the same value, we’ll give them both the same label and we’ll call each of these angles 𝜃. Now, from our law of reflection, we know that 𝜃 𝑖 is equal to 𝜃 𝑟. We also know that the orange triangle has a second angle equal to 𝜃 𝑖 and the blue triangle has a second angle equal to 𝜃 𝑟. Both of these triangles are right-angled triangles as they have one angle that is 90 degrees. The first one here is drawn in orange and the second one in blue. If we look again at our diagram, we see that we can define two triangles. Or in terms of symbols, the law says that 𝜃 𝑖 is equal to 𝜃 𝑟. What the law of reflection says is that the angle of incidence is equal to the angle of reflection. Similarly, the angle between the reflected ray and the same normal to the surface is known as the angle of reflection and is often labeled as 𝜃 𝑟. The angle between the incident light ray and the normal to the surface is known as the angle of incidence and is commonly labeled as 𝜃 𝑖. That is, it meets the surface at an angle of 90 degrees.

The normal is a line that is perpendicular to the surface. In the diagram from the question, the normal to the surface is this dashed line. At the point where the incident ray meets the reflecting surface, we can draw something called the normal to the surface. This law is known as the law of reflection, and it works as follows. We can recall that when light reflects from a surface, it does so according to a particular law. Finally, this gray rectangle here is the mirror that the light ray reflects from. Looking at the diagram, this right here is the incident light ray and this here is the reflected ray. So, this question is about a light ray reflecting from a mirror. The length 𝐴𝐵 equals four centimeters, the length 𝐵𝐶 equals four centimeters, and the length 𝐶𝐸 equals five centimeters. The angle of incidence and angle of refraction are mathematically related to the index of refraction of each material through the law of refraction, also called Snell’s Law.A light ray reflects from a mirror, as shown in the diagram. Unlike reflection, the angle of incidence is not equal to the angle of refraction. If light is traveling in one material and then refracts in a second material, it will bend towards the normal if the index of refraction of the second material, n 2, is greater than the index of refraction of the first material, n 1 (the light travels slower in the second material) ( n 1 n 2) (B). The higher the index of refraction, the slower light travels in that medium.

The index of refraction of a material is equal to the speed of light in a vacuum, divided by the speed of light in the material. Materials have a property called the index of refraction, which is symbolized using the letter n. Shopping cart example of refraction (©2020 Let’s Talk Science).